池状構造物【地下構造物】の曲げ・せん断照査における耐震計算法の特徴比較
本資料は指針本編「4.5 池状コンクリート構造物の耐震計算と性能照査 4.5.3 耐震計算の方針」等に関し て、ケーススタディを通じて地下式池状構造物に適用する静的計算法と動的非線形解析の適用範囲および解 析結果に見られる特徴等を記載したものである。 池状構造物の耐震計算において構造物の曲げ損傷やせん断破壊を照査するにあたっては、三次元効果の有 無やその程度および設計地震動の特性なども踏まえ、最適な耐震計算法を選択する必要がある。そして、確 実に所定の性能を確保しつつ、かつ合理的な耐震設計が可能となる耐震計算法を選択し、それぞれの設計実 務において手法の選定を検討する必要がある。 ここでは、設計実務において耐震計算法を選択する際の参考として、地下構造物を対象に、三次元性の影 響や設計地震動の特性をパラメータとした比較解析の結果を示す。そして、地盤―構造物連成系モデルを用 いた動的非線形解析の結果を最も精度の高い解析結果とした場合の、構造物独立モデルを用いた静的解析 (震度法、応答変位法)や設計地震動方法 4 の適用範囲に関する検討を行う。 なお、本検討の主な目的は以下のとおりである。 1)本検討の主な目的 耐震計算において所定の性能を確実に確保することや、経済的な断面(部材厚、鉄筋量)を設定するこ とができる静的解析などの簡便な耐震計算方法の適用範囲の傾向を以下の視点から把握する。 ① 視点 1 池状構造物の構造形状の違い 地震作用に対して、構造物全体系の挙動は、三次元効果が大きい場合は弾性的になり、三次元効果が小 さい場合は非線形性の影響が大きくなる。それによって、静的解析(震度法、応答変位法)による線形解 析や非線形解析の適用限界が見られることが考えられる。 ② 視点 2 設計地震動の違い 設計地震動の大きさや周期特性によって、動的解析と静的解析結果の差異に影響がある。それによって、 設計地震動の違いによる静的解析の適用限界や、方法 4 の設計地震動の適用限界が見られることが考えら れる。 このようなことから、本検討においては、池状構造物の三次元性(構造形状)や設計地震動をパラメー タとして耐震計算法の比較検討を行った。これらの詳細な理由を以下に示す。 【構造物の三次元性をパラメータとする理由】 池状構造物の地震時挙動(発生曲げモーメントや発生せん断力など)は、池状構造物の三次元的な構 造特性の影響を大きく受ける傾向がある。すなわち、二次元の解析モデルにおいても、モデルの妻側に ある側壁や隔壁などの剛性が大きくなるに従い、構造全体系のせん断変形を抑制する効果が大きくな り、曲げひずみやせん断力の発生を小さくする傾向がある。過去の地震において池状構造物の損傷被害 が殆ど確認されていない要因として、その三次元的な効果が考えられる。よって、池状構造物の耐震設 計においては、この三次元的な特性を適切に評価することが重要である。 設計実務においては、三次元モデルや三次元効果を考慮した二次元モデルの適用を行い、合理的な耐 震設計を行うことができる場合がある。その一方、三次元効果を考慮しない方が安全側の設計となる傾 向に着目し、対象構造物の構造形状に関係なく、三次元性を考慮しない場合も多い。ただし、三次元性 の考慮の有無については、そもそも構造モデルにおける力学的特性が異なることに留意し、最適な構造 計画や耐震設計を行う必要がある。 妻壁や耐震壁などの三次元効果を考慮する構造の場合は、地震作用を構造物全体の剛性により対応す る傾向が強くなるが、三次元効果を考慮しない構造の場合は、部材の非線形化に伴う地震エネルギー低 減効果によって対応する傾向が強くなる。そのため、池状構造物の耐震設計にあたっては、池状構造物 の三次元的な力学的特性を十分に検討し、より合理的な構造計画にするとともに、その構造的な特性と 整合性の高い最適な解析手法や解析モデルを選択する必要がある。 【設計地震動をパラメータとする理由】 池状構造物に適用する静的解析と動的解析の解析結果の違いや構造物特性係数の一般値の適用性につ いては、設計地震動によっても異なる傾向がある。すなわち、設計地震動の加速度の大きさや周期特性 の違いによって、静的解析で動的解析を代替できる範囲が変わってくることや、構造物特性係数の一般 値の適用性に注意することが重要である 2.検討の基本条件 検討対象構造物の基本条件は、図-参3-6.1および表-参3-6.1~2に示すとおりである。 1)構造条件 ① 地下式配水池(有蓋)、フラットスラブ構造。 ② 構造物形状(L/B)や(B/H)、および(L/H)を、パラメータとして、複数の耐震計算法と複数の設 計地震動を適用して解析を実施する。 2)地盤条件 ① 対象地盤は地表面から深さ7.55m までが N 値 5 の沖積砂質土層で、その下部が N 値50以上の洪積砂 礫層とし、洪積砂礫層を工学的基盤面とする。 ② 耐震設計上の地盤種別はⅡ種地盤とし、地下水位は工学的基盤面である洪積砂礫層より深い位置とす る。 3)設計地震動 ① 対象構造物のレベル 2 地震動は方法 3 に従い、工学的基盤面が路頭する地盤条件における深度 6 強~ 震度 7 の強震記録より 2 波形を選定する。一つは、「コンクリート標準示方書」に示されている内陸型地 震の波形加速度の中から1995年兵庫県南部地震におけるポートアイランドでの観測波形を基に算出した 243 3 .構造物 解放基盤の地震動(以降、ポートアイランド基盤波と称す)、もう一つは JR 鷹取駅観測記録の引き戻し により算出した解放基盤の地震動(以降、JR 鷹取駅基盤波と称す)とする。 ② 静的線形解析に用いる入力地震動は、方法 4 により算出した設計震度と一次元地盤応答解析により算 出した最大応答加速度を用いて表現する。なお、Ⅱ種地盤相当の方法 4 で設定した設計水平震度は kh02 =0.80、ポートアイランド引き戻し波の最大地表面加速度は700gal であり、おおむね同等であるが、方 法 4 のほうがやや大きくなる。一方、JR 鷹取駅引き戻し波は周期特性が異なる。 ③ 応答変位法に用いる入力地震動は、方法 4 により算出した地盤変位と一次元地盤応答解析により算出 した頂版と底版深さ間の水平方向相対変位が最大となる時刻における応答値(加速度、変位、せん断応 力)を用いて表現する。 ④ 動的非線形解析の入力地震動は加速度時刻歴波形で表現する。
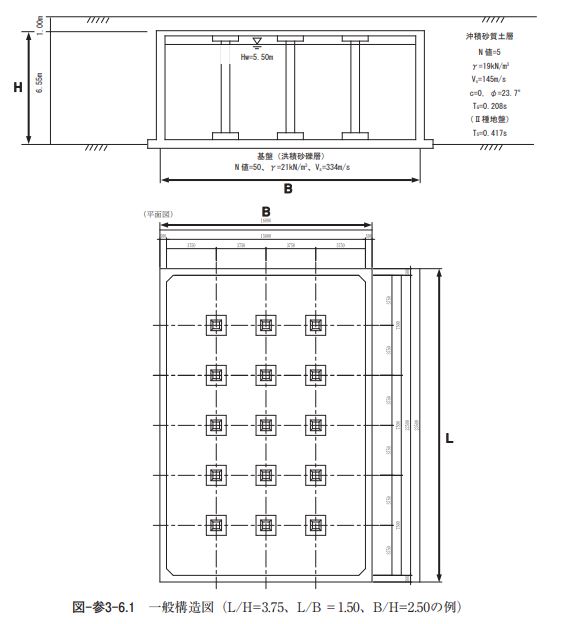
4)材料条件
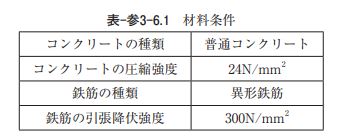
5)断面条件
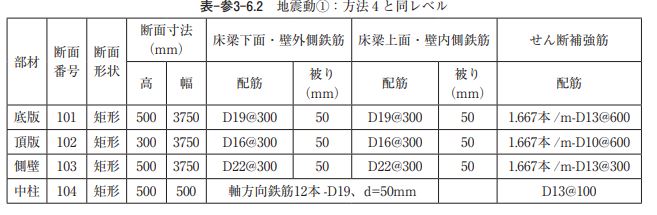
6)耐震計算法 耐震計算法は、次の 4 ケースの耐震計算法を適用する。 ① 静的線形解析(構造物特性係数 Cs を考慮しない) ② 応答変位法(線形モデル) ③ 応答変位法(非線形モデル) ④ 動的非線形解析(地盤-構造物連成系モデル)
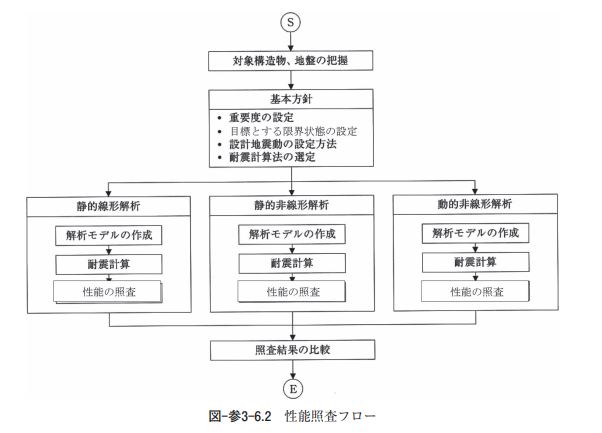
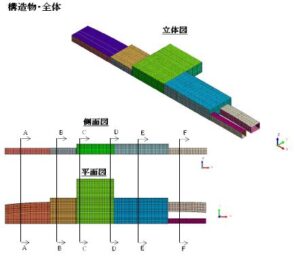
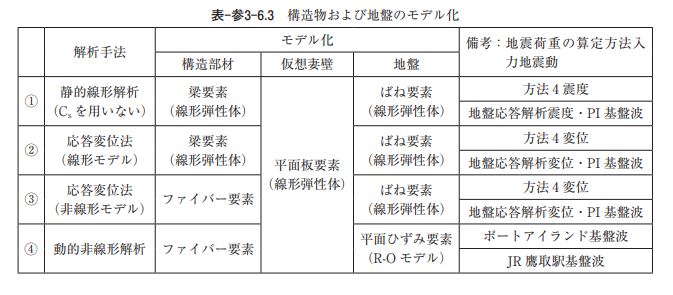
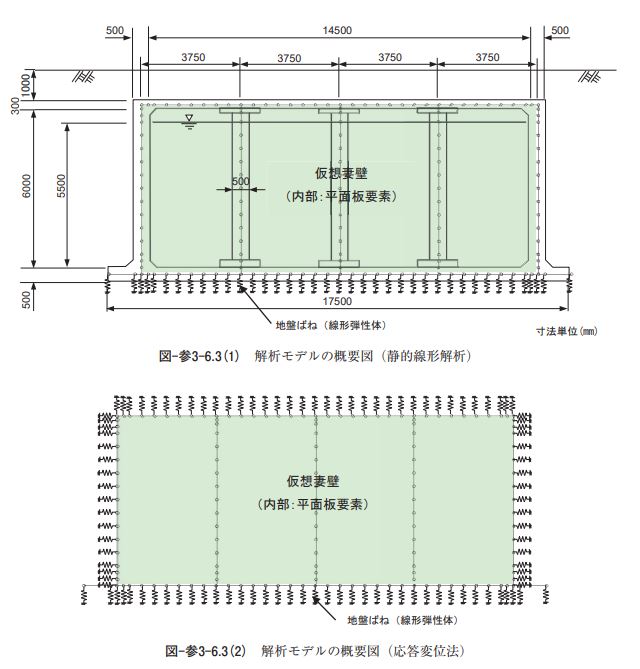
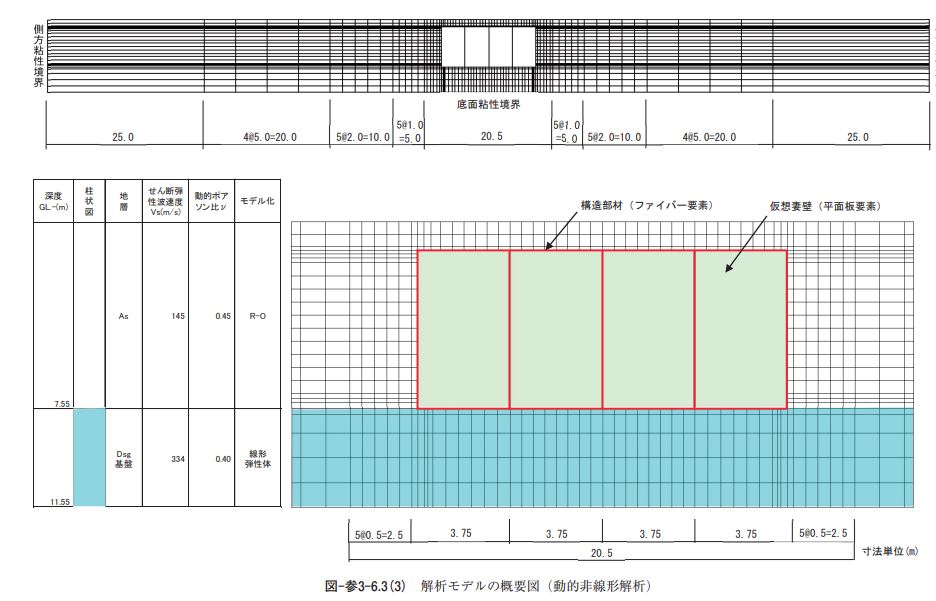
・静的線形解析 対象構造物は躯体全体が完全に地中にあるが、周辺地盤の地震時挙動による影響よりも地震動による躯 体慣性力や動水圧の影響が大きい可能性がある場合を想定し、震度法を適用する。ただし、静的線形解析 では、構造物の塑性変形能力によるエネルギー吸収性能を構造物特性係数(Cs)により考慮しないものと する。 ・応答変位法 対象構造物は躯体全体が完全に地中にあり、地震動による躯体慣性力や動水圧の影響よりも周辺地盤の 地震時挙動による影響に支配される傾向が強いと考えられることから、応答変位法を適用する。②応答変 位法(線形モデル)では、構造物を梁要素にモデル化し、これを周辺地盤との相互作用を表すバネで支持 する線形計算法を採用する。一方、③応答変位法(非線形モデル)では、各部材・部位毎の局所的な損傷 状態を詳しく把握することを目的に、構造物をファイバー要素にモデル化し、これを周辺地盤との相互作 用を表すバネで支持する非線形計算法を採用する。 ・動的非線形解析 動的非線形解析の場合は、材料非線形性を適切に考慮し、時々刻々と変化する地盤や構造物の剛性や減 衰を追跡可能な時刻歴応答解析(直接積分法)を適用する。動的非線形解析の入力地震動は、地下構造物 の耐震性に及ぼす入力地震動の周期特性等の影響を確認するため、ポートアイランド基盤引き戻し波と JR 鷹取駅基盤引き戻し波の 2 波形を採用する 3.解析条件 1)解析モデル 解析モデルは構造物中央部における二次元鉛直断面モデルとし、解析モデルの奥行き幅は中柱中心間隔 の3.75m とする。図-参3-6.3に解析モデルの概要図、表-参3-6.3に構造物および地盤のモデル化の概要を示 す。 底版、頂版、側壁および中柱は、表-参3-6.3に示す梁要素またはファイバー要素にモデル化する。梁要 素とファイバー要素の軸線はハンチやドロップパネル等の影響を無視し、構造部材の軸線に沿って一直線 に配置する。側壁と底版との接合部等の隅角部や交差部には剛域を設ける。 二次元モデルにおける三次元効果の影響は、池の内空部分に配置する仮想妻壁(平面板要素)により表 現する。平面板要素の板厚 t、単位体積重量γおよびポアソン比νは、解析手法や入力地震動が異なるす べてのケースで t=0.5m、γ=0、ν=0.2とする。 地盤は、動的非線形解析以外では線形ばね要素にモデル化する。地盤ばね定数は N 値より推定した地盤 反力係数に分担面積を乗じて算出する。地盤ばね定数はすべてのケースで共通とする。動的非線形解析で は,地盤を平面ひずみ要素にモデル化し、地盤のせん断応力~せん断ひずみ関係に Ramberg-Osgood モデ ル(以下 R-O モデル)を採用する。なお、動的非線形解析では構造物底版が工学的基盤面上に位置する状 態となるため、解析モデルの底版下部に厚さ4.0m の基盤層(線形弾性体)をモデル化することにより底面 境界による影響の軽減を図る。 内水は自由水面を有する矩形水槽の動水圧分布に基づいて分布荷重または付加重量にモデル化し、常時 荷重時の静水圧は分布荷重として底版、側壁に作用させる。 静的線形解析および応答変位法(線形モデル)では、構造部材を線形梁要素にモデル化する。静的線形 解析に用いる構造部材の断面定数はコンクリート全断面有効として算出する。 応答変位法(非線形モデル)および動的非線形解析では、構造部材をファイバー要素にモデル化する。 ファイバー要素の材料特性は、コンクリートの応力~ひずみ関係に修正 Ahmad 式を、鉄筋の応力~ひず み関係にバイリニアモデル(移動硬化)を採用する
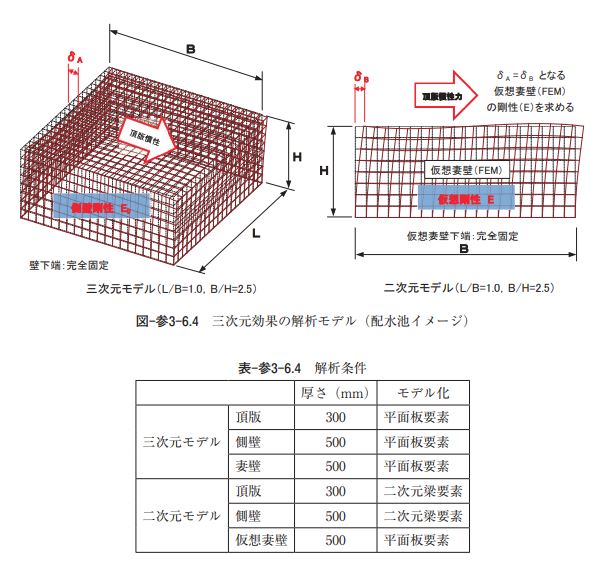
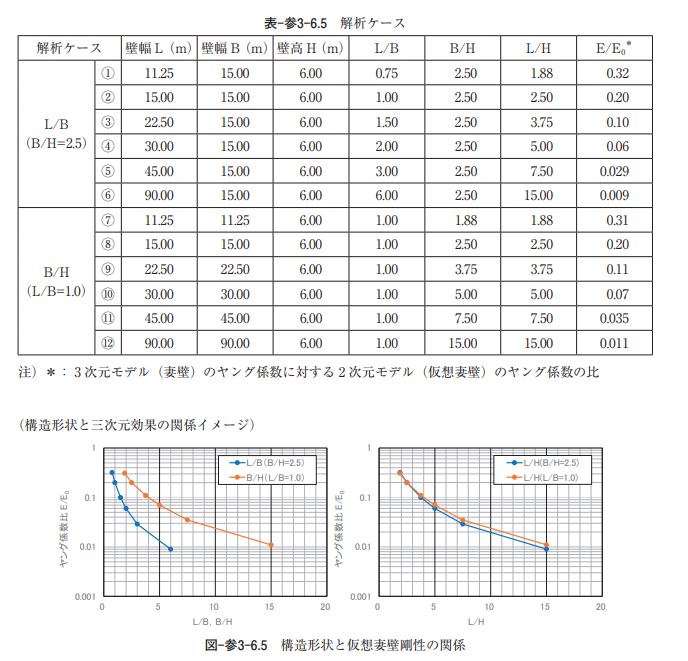
なお、本検討における構造形状の違いによるパラメータについては、まず、表-参3-6.5に示すように構 造形状の(L/B)と(B/H)をパラメータとして、12ケースの二次元モデルにおける三次元効果を表現す る池内空間の平面板要素の剛性(ヤング係数比(E/E0)= 二次元モデルの仮想壁のヤング係数 / 実際(三 次元モデル)の側壁のヤング係数)を求めた。その関係図を図-参3-6.5に示す。 構造形状の違いを示すパラメータについては、(L/B)と(B/H)、さらにそれらを合成した(L/H)な ど複数ある。ただし、図-参3-6.5に示すように、(L/B)をパラメータとして求めたヤング係数比と(B/H) をパラメータとして求めたヤング係数比について、それぞれの結果を(L/H)をパラメータとして表現す ると、ほぼ同値となることから、(B)の影響はほとんどないものと考えることができる。そのため、以降 の検討においては(L/H)をパラメータとして検討を行うものとする。これは、実際の耐震設計において も、三次元効果を評価するにあたっては、(L/H)に注目することが重要であることを意味しており、他の 基準書(鉄道標準トンネル編)においても、(L/H)に着目し、耐震計算における解析モデルでの三次元効 果の考慮の有無を評価することとしている(L/H = 5 以下の場合に三次元効果を考慮することとしてい る)
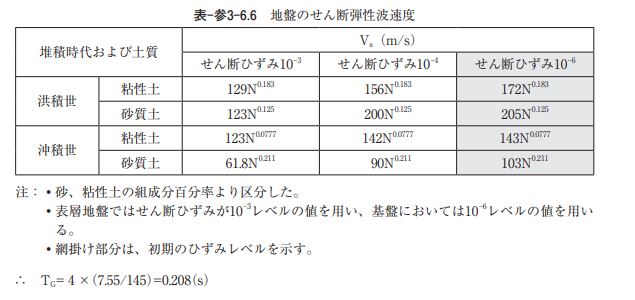
2)設計地震動 (1)静的線形解析 ① 方法 4 による場合 ア)地盤固有周期 地盤固有周期は、次式により算出する。ここに,TG:地盤固有周期(s) Hi :i 番目の地層の層厚(m) Vsi:i 番目の地層の平均せん断弾性波速度(m/s)で、本計算例では標準貫入試験の平均 N 値 を用いて表-参3-6.6により推定する。 沖積砂質土層:Vs=103×(5)0.211=145m/s
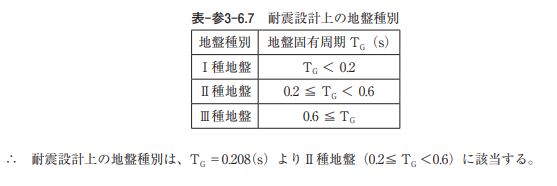
イ)耐震設計上の地盤種別 耐震設計上の地盤種別は、地盤固有周期を用いて表-参3-6.7により判定する。
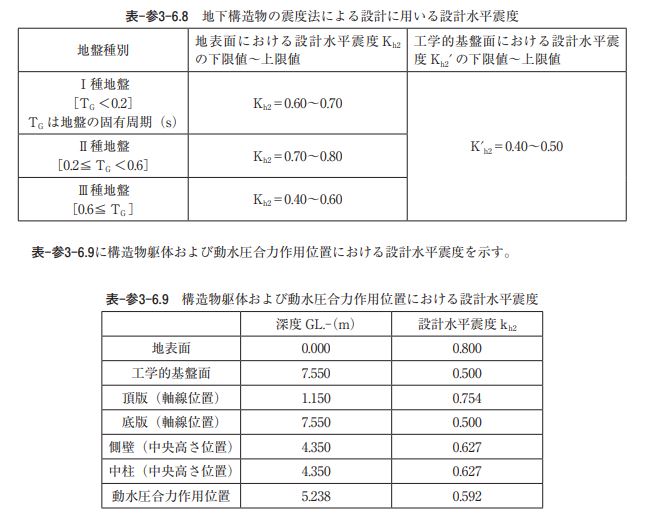
ウ)設計水平震度 設計地震動は、表-参3-6.8に示す地盤種別に応じた地表面と工学的基盤面における設計水平震度の上限 値を用いて、線形補間により構造物躯体(底版、頂版、側壁、中柱)と動水圧合力作用位置の地中深さに おける設計水平震度を算定する。このとき、構造物特性係数は用いないものとし、動水圧合力作用位置は 底版上面から全水深 Hw の 3/8 の高さとする。
② 地盤応答解析による場合 ア)入力地震動 地盤応答解析の入力地震動は、方法 3 に従い、工学的基盤面が路頭する地盤条件における震度 6 強~震 度 7 の強震記録より、「コンクリート標準示方書」に示されている内陸型地震の加速度波形の中から1995年 兵庫県南部地震におけるポートアイランド基盤波を選定する。 動的解析に用いるレベル 2 地震動について、図-参3-6.6に時刻歴波形とその応答スペクトル(減衰定数 5 %と10%)を示す。
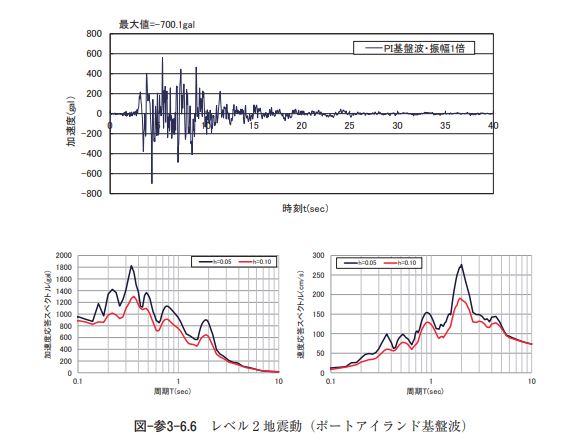
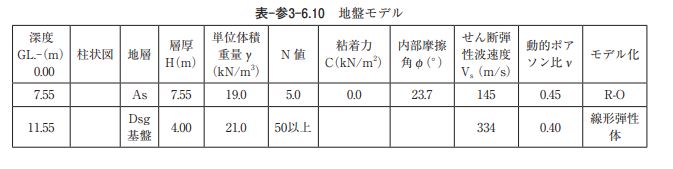
イ)地盤モデル 対象地盤は地表面から深さ7.55m までが N 値 5 の沖積砂質土層で、その下部が N 値50以上の洪積砂礫 層とする。工学的基盤面は洪積砂礫層上面とし、地下水位は洪積砂礫層より深い位置とする。なお、動的 非線形解析では構造物底版が工学的基盤面に位置する状態になるため、解析モデルの底版下部に厚さ4.0m の基盤層(線形弾性体)をモデル化することにより底面境界による影響の軽減を図ることとした。 これより、地盤応答解析に用いる地盤モデルは、動的非線形解析と同様に沖積砂質土層下部に基盤層が 存在する 2 層構造地盤とする。工学的基盤面より上部の沖積砂質土層は非液状化層とし、動的非線形解析 と同様に地震応答解析で実績の多い R-O モデルにより表現する。また,基盤層も動的非線形解析と同様に 線形弾性体により表現する。 各地層の単位体積重量は土質に応じた一般値とし、各地層のせん断弾性波速度 Vs は表-参3-6.10に示す N 値による推定値(せん断ひずみ10-6レベル)とする。また、沖積砂質土層の動的ポアソン比は0.45、基盤 層は0.40とする。 以上の方法により設定した地盤モデルを表-参3-6.10に示す。
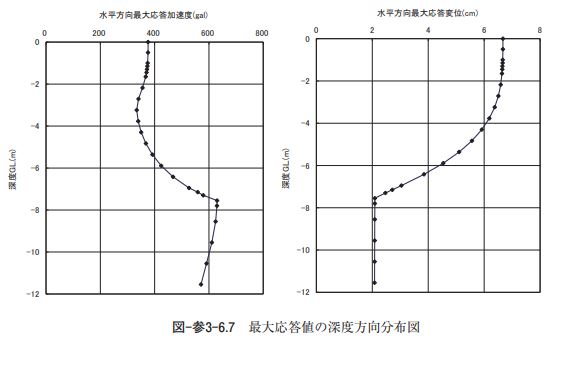
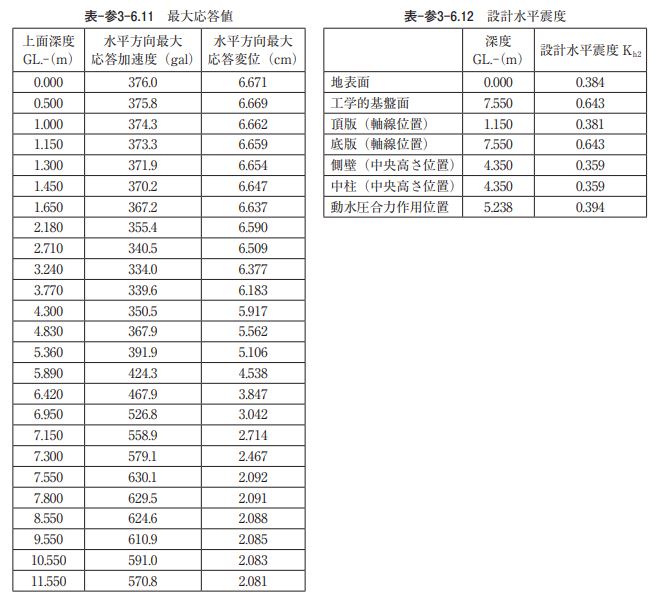
ウ)応答解析結果 地盤応答解析結果より、図-参3-6.7、表-参3-6.11に最大応答加速度と最大応答変位の深度方向分布図と これらの最大応答値の値を示す。 設計水平震度は、表-参3-6.11に示す最大応答加速度を用いて線形補間により構造物躯体(底版、頂版、 側壁、中柱)と動水圧合力作用位置の地中深さにおける設計水平震度を算定する。このとき、構造物特性 係数は用いないものとし、動水圧合力作用位置は底版上面から全水深 Hw の 3/8 の高さとする。表-参 3-6.12に構造物躯体および動水圧合力作用位置における設計水平震度を示す。
(2)応答変位法 ① 方法 4 による場合 ア)地盤固有周期 地盤固有周期 は、静的線形解析と同一の方法により算出する。 ∴ TG= 4 ×(7.55/145)=0.208(s) イ)表層地盤の固有周期 表層地盤の固有周期は、地震時における地盤のひずみレベルによる剛性低下を考慮し、地震動規模に応 じて次式により算定する。 レベル 2 地震動:TS = 2.00TG ∴ TS = 2.00×0.208=0.417(s) ウ)設計応答速度 設計応答速度は、図-参3-6.8に示す基盤地震動の設計用速度応答スペクトル図を用いて表層地盤の固有 周期に対応する上限値の値を算出する
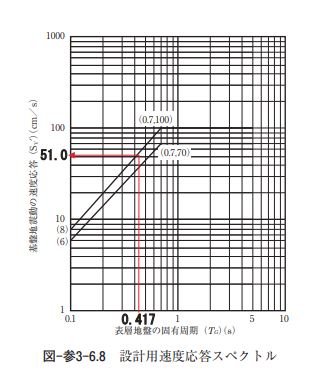
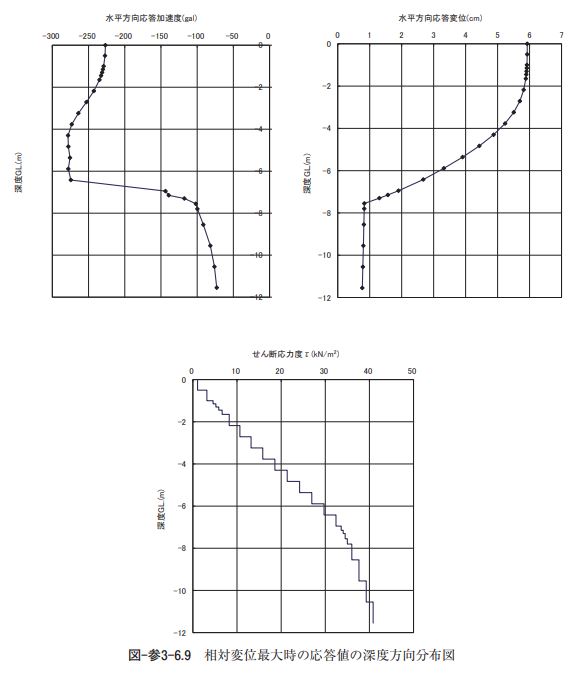
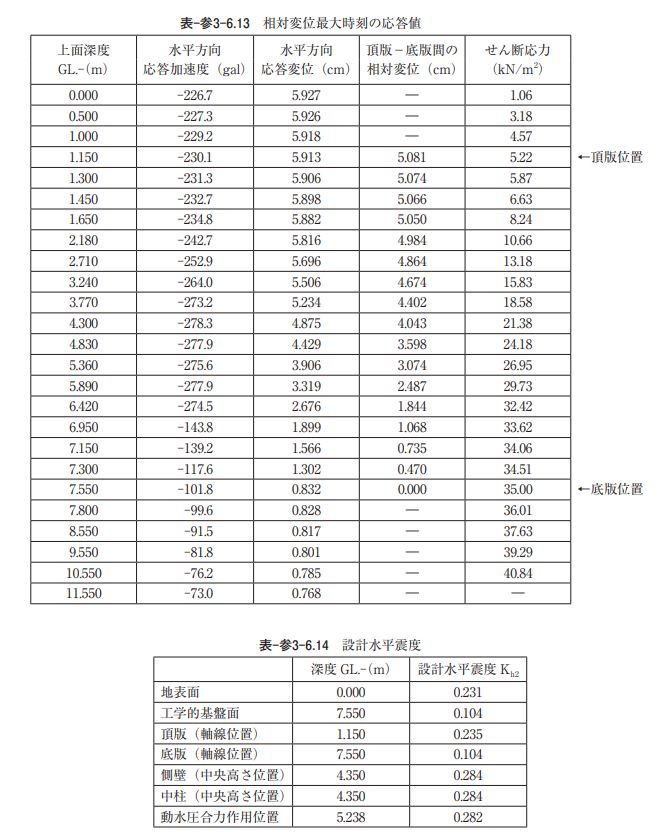
②地盤応答解析による場合 ア)入力地震動 地盤応答解析の入力地震動は、静的線形解析と同一(ポートアイランド基盤波)とする。 イ)地盤モデル 地盤モデルは静的線形解析と同一とする。 ウ)応答解析結果 地盤応答解析結果より、頂版-底版間の水平方向相対変位が最大時刻における応答値を用いて地震荷重 (慣性力、動水圧、地盤変位、周面せん断力)を算定する。図-参3-6.9に頂版-底版間の水平方向相対変位 が最大時刻における応答値(応答加速度,応答変位および応答せん断応力度)の深度方向分布図を示す。 また、表-参3-6.13にはこれらの応答値と頂版-底版間の水平方向相対変位を示す。 設計水平震度は、静的線形解析の場合と同様に表-参3-6.13に示す応答加速度を用いて、線形補間により 構造物躯体(底版、頂版、側壁、中柱)と動水圧合力作用位置の地中深さにおける設計水平震度を算定す る。表-参3-6.14に構造物躯体および動水圧合力作用位置における設計水平震度を示す。なお、設計水平震 度は、慣性力や動水圧が応答加速度と逆向きに作用することを考慮して符号を表示している。
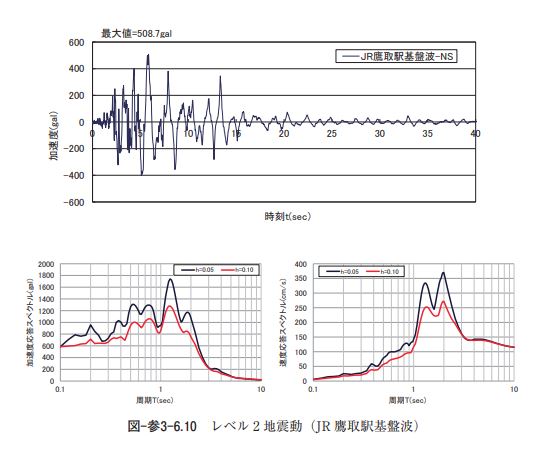
(3)動的非線形解析 ア)入力地震動 動的非線形解析の場合、レベル 2 地震動は方法 3 に従い、工学的基盤面が路頭する地盤条件における震 度 6 強~震度 7 の強震記録より、「コンクリート標準示方書」に示されている内陸型地震の加速度波形の中 259 3 .構造物 から1995年兵庫県南部地震におけるポートアイランド基盤波、JR 鷹取駅基盤波を選定する。 動的解析に用いるレベル 2 地震動について、図-参3-6.10に JR 鷹取駅基盤波の時刻歴波形とその応答ス ペクトル(減衰定数 5 %と10%)を示す。なお、もう一つのポートアイランド基盤波は、前述の静的線形 解析で示した図-参3-6.6と同一とする。 イ)地盤モデル 地盤モデルは静的線形解析と同一とする。
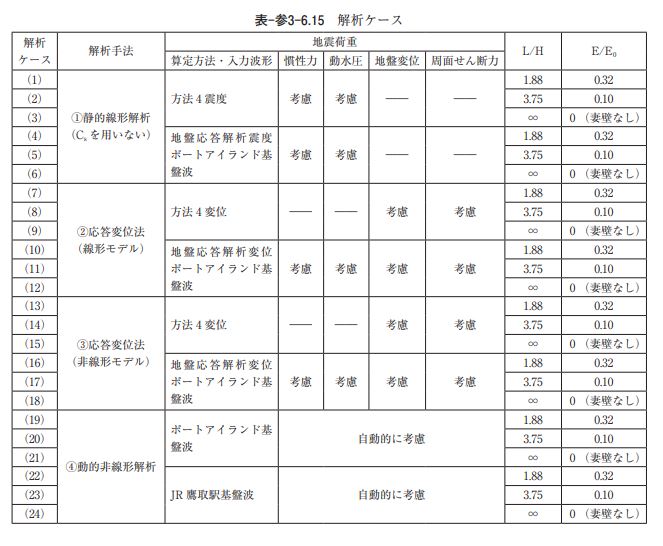
4.耐震計算 1)解析ケース 構造形状に関するパラメータや設計地震動のパラメータを考慮した解析ケースを表-参3-6.15に示す。 解析ケースは、それぞれの 4 ケースの耐震計算法に対して、設計地震動 2 ケース、構造物形状(L/H) を 3 ケースの全24ケース(= 4 × 2 × 3 )とした。
2)照査方法 (1)曲げに対する照査 限界状態 2 の照査として、鉄筋コンクリート部材の曲げに対する照査は、部材の応答曲げモーメントを 用いて次式により判定する。
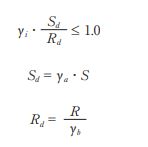
ここに、Sd :照査応答値 Rd:照査限界値 S :部材の応答値で、要素中央における応答曲げモーメントとする。 R :限界状態 2 における部材の断面耐力で、要素中央における応答軸力作用時の最大耐荷力点 の曲げモーメント Mu とする。 γi :構造物係数(=1.0) γa:構造解析係数(=1.0) γb:部材係数(=1.0) (2)せん断破壊に対する照査 鉄筋コンクリート部材のせん断破壊に対する照査は、次式により判定する。

γb :部材係数(=1.1×1.0=1.1)
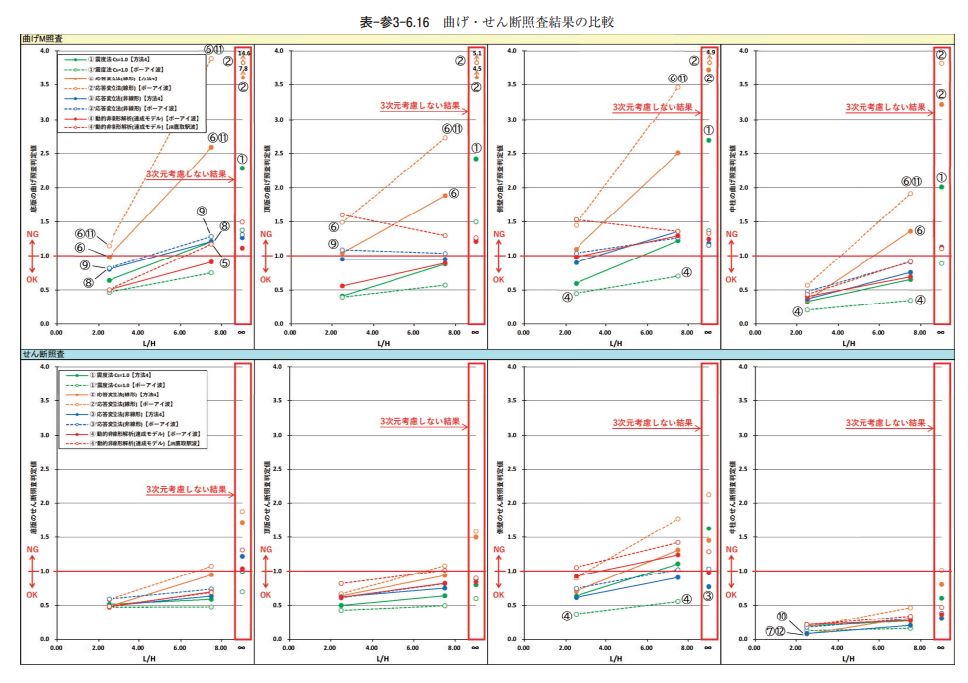
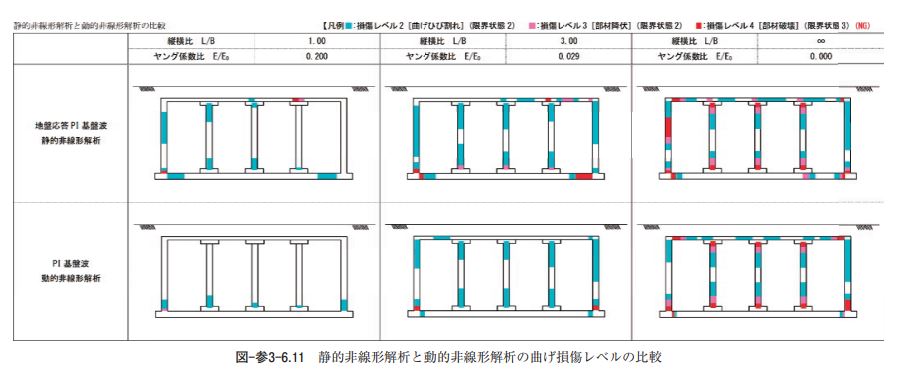
3)計算結果 計算結果として、各耐震計算法における各部材の曲げ・せん断力の照査指標値(OK―NG 判定値)の最 大値についての比較を表-参3-6.16に示す。また、静的非線形解析と動的非線形解析の曲げ損傷レベルの比 較図を図-参3-6.11に示す。
5.考察 1)まとめ 地下構造物は三次元性の考慮の有無、また設計地震動によって、各耐震計算法の特徴は大きく異なる傾 向があることから、それぞれの特徴について示す。 (1)三次元性を考慮しない構造物 三次元性を考慮しない構造物の耐震計算において、震度法と応答変位法ともに、線形モデル適用の場合 は、動的非線形解析(連成系モデル)に比べて安全側の解析結果となる傾向がある。ただし、曲げ照査に おいて、過大な設計となる場合も想定され、これらの耐震計算法の適用にあたっては、経済性への影響評 価が重要である。そのため、設計実務においては、経済性への配慮から比較的規模の小さな構造物への適 用が有効と考える。特に、応答変位法を適用する場合は、その傾向が強いことに留意する必要がある。ま た、設計地震動の影響が方法 4 を大きく上回る場合は安全側の設計の面で留意が必要であり、できるだけ 地盤応答解析を事前に行い、地震の影響を評価するのが望ましい。 応答変位法において非線形モデルを適用する場合は、震度法や線形モデルを適用する場合に比べて、動 的非線形解析(連成系モデル)の結果とかなり整合する傾向にある。そのため、構造規模に関係なく広く 適用できると考える。ただし、方法 4 の変位振幅による設計地震動を適用した場合には、動的非線形解析 と比べて安全側の設計となる場合もあれば、危険側の設計となる場合もあることに留意が必要である。一 方、地盤応答解析の結果を適用した設計地震動を用いる場合は、安全側の設計や経済設計の実施の観点か ら設計の精度が向上する傾向があり有効である。 (2)三次元性を考慮する構造物 三次元性を考慮する構造物の耐震計算において、震度法を適用する場合は、動的非線形解析(連成系モ デル)を適用した解析結果と比べて危険側の設計になる部材が多くなる場合があり、その適用にあたって は十分な安全性の配慮が必要である。特に方法 4 を上回る地震作用を与える設計地震動を用いる場合に は、かなり危険側の設計となる場合があることに注意が必要である。 応答変位法において線形モデルを適用する場合は、構造形状(三次元効果の程度)に関係なく、方法 4 と同等の地震作用を与える設計地震動を用いる場合であれば、おおむね安全側の設計となる傾向がある。 ただし、構造形状(三次元効果の程度)によっては、曲げ照査において、かなり過大な設計となる場合が あり、これらの耐震計算法の適用にあたっては、経済性への影響評価が重要であり、経済性への配慮から 比較的規模の小さな構造物への適用が有効と考える。なお、方法 4 を上回る地震の影響を与える設計地震 動の場合は、危険側の設計となる傾向があることにも留意し、十分な安全側の設計への配慮が必要である。 そのため、できるだけ地盤応答解析を事前に行い、地震の影響を事前に評価することが望ましい。 応答変位法において非線形モデルを用いる場合は、動的非線形解析の結果と整合する傾向はあるが、危 険側の設計となる場合があることから、設計上の余裕の確保が必要である。一方、設計地震動を用いた地 盤応答解析の結果を適用した場合には、設計精度が向上するため有効である。ただし、この場合でも、や や危険側の設計となる場合があることから、設計上の余裕の確保は必要と考える。